백준 1006번
오늘 풀어본 문제는 백준의 1006번 문제1이다. 문제 풀이에 사용한 언어는 C++ 이다.
solved.ac 기준 CLASS
문제 정보
이 문제의 내용과 조건은 다음과 같다.
문제
초라기는 한국의 비밀국방기지(원타곤)를 습격하라는 임무를 받은 특급요원이다. 원타곤의 건물은 도넛 형태이며, 초라기는 효율적인 타격 포인트를 정하기 위해 구역을 아래와 같이 두 개의 원 모양으로 나누었다. (그림의 숫자는 각 구역의 번호이다.)
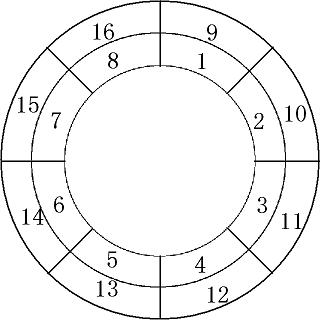
초라기는 각각 $W$ 명으로 구성된 특수소대를 다수 출동시켜 모든 구역에 침투시킬 예정이며, 각 구역 별로 적이 몇 명씩 배치되어 있는지는 초라기가 모두 알고 있다. 특수소대를 아래 조건에 따라 침투 시킬 수 있다.
-
한 특수소대는 침투한 구역 외에, 인접한 한 구역 더 침투할 수 있다. (같은 경계를 공유하고 있으면 인접 하다고 한다. 위 그림에서 $1$ 구역은 $2$, $8$, $9$ 구역과 서로 인접한 상태다.) 즉, 한 특수소대는 한 개 혹은 두 개의 구역을 커버할 수 있다.
-
특수소대끼리는 아군인지 적인지 구분을 못 하기 때문에, 각 구역은 하나의 소대로만 커버해야 한다.
-
한 특수소대가 커버하는 구역의 적들의 합은 특수소대원 수 $W$ 보다 작거나 같아야 한다.
이때 초라기는 원타곤의 모든 구역을 커버하기 위해 침투 시켜야 할 특수 소대의 최소 개수를 알고 싶어 한다.
입력
첫째 줄에 테스트 케이스의 개수 $T$ 가 주어진다. 각 테스트 케이스는 다음과 같이 구성되어있다.
첫째 줄에는 $(\text{구역의 개수})/2$ 값 $N$ 과 특수 소대원의 수 $W$ 가 주어진다. $(1 \le N \le 10000, 1 \le W \le 10000)$.
둘째 줄에는 $1 \sim N$ 번째 구역에 배치된 적의 수가 주어지고, 셋째 줄에는 $N+1 \sim 2N$ 번째 구역에 배치된 적의 수가 공백으로 구분되어 주어진다. $(1 \le \text{각 구역에 배치된 최대 적의 수} \le 10000)$ 단, 한 구역에서 특수 소대원의 수보다 많은 적이 배치된 구역은 존재하지 않는다. (따라서, $\text{각 구역에 배치된 최대 적의 수} \le W$)
출력
각 테스트케이스에 대해서 한 줄에 하나씩 원타곤의 모든 구역을 커버하기 위해 침투 시켜야 할 특수 소대의 최소 개수를 출력하시오.
풀이과정
1번째 시도
문제를 보고 끔찍한 DP 문제라는 것을 알 수 있었다. 점화식을 세운 아이디어는 다음과 같다.
-
dp배열의 인덱스의 의미:dp배열은 2차원 배열로 되어있다.첫 번째 인덱스는 원타곤을 일자로 폈다고 생각했을 때 첫 번째 칸들과 마지막 칸들을 ‘연결시켜’ 소대를 파견했는가에 대한 정보를 담는다.
두 번째 인덱스는 원타곤을 일자로 폈다고 생각했을 때 특정 번재 칸들까지 점령하는데 필요한 최소 소대의 개수를 담는다. 이 때 같은 번째 칸들까지라고 하더라도 첫 번째 인덱스의 값에 따라 필요한 소대의 수가 달라질 수 있다.
-
점화식 구조: 이전 두 인덱스 칸들의 소대수를 활용하여 현재 칸과 바로 직전 칸을 연결시킬 수 있는지 확인하고, 현재 칸들끼리 결합하는 경우가지 고려하여 가장 적은 소대수를 얻을 수 있는 경우를 저장하도록 점화식을 구성하였다.
코드는 다음과 같이 작성하였다.
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
using ull = unsigned long long;
using pii = pair<int, int>;
using pll = pair<ll, ll>;
void simulate();
int main(void) {
ios::sync_with_stdio(false);
cin.tie(nullptr);
cout.tie(nullptr);
int T;
cin >> T;
for (int i=0; i<T; i++) {
simulate();
}
return 0;
}
void simulate() {
int N, W;
cin >> N >> W;
vector<int> enemy[2];
enemy[0].resize(N);
enemy[1].resize(N);
for (int i=0; i<N; i++) {
cin >> enemy[0][i];
}
for (int i=0; i<N; i++) {
cin >> enemy[1][i];
}
vector<vector<int>> dp(4, vector<int>(N, INT_MAX));
for (int option=0; option<4; option++) {
switch (option) {
case 0: // Separated up and down
dp[option][0] = 1 + (enemy[0][0] + enemy[1][0] > W);
dp[option][1] = min({
dp[option][0] + 1 + (enemy[0][1] + enemy[1][1] > W),
2 + (enemy[0][0] + enemy[0][1] > W) + (enemy[1][0] + enemy[1][1] > W)
});
break;
case 1: // Merged up and Separated down
dp[option][0] = 2;
dp[option][1] = min({
dp[option][0] + 1 + (enemy[0][1] + enemy[1][1] > W),
3 + (enemy[1][0] + enemy[1][1] > W)
});
break;
case 2: // Separated up and Merged down
dp[option][0] = 2;
dp[option][1] = min({
dp[option][0] + 1 + (enemy[0][1] + enemy[1][1] > W),
3 + (enemy[0][0] + enemy[0][1] > W)
});
break;
case 3: // Merged up and down
dp[option][0] = 2;
dp[option][1] = dp[option][0] + 1 + (enemy[0][1] + enemy[1][1] > W);
break;
default:
break;
}
for (int i=2; i<N-1; i++) {
dp[option][i] = min({
dp[option][i-1] + 1 + (enemy[0][i] + enemy[1][i] > W),
dp[option][i-2] + 2 + (enemy[0][i-1] + enemy[0][i] > W) + (enemy[1][i-1] + enemy[1][i] > W)
});
}
switch (option) {
case 0:
dp[option][N-1] = min({
dp[option][N-2] + 1 + (enemy[0][N-1] + enemy[1][N-1] > W),
dp[option][N-3] + 2 + (enemy[0][N-2] + enemy[0][N-1] > W) + (enemy[1][N-2] + enemy[1][N-1] > W)
});
break;
case 1:
dp[option][N-1] = min({
dp[option][N-2] + 2 + (enemy[0][N-1] + enemy[0][0] > W) - 1,
dp[option][N-3] + 3 + (enemy[0][N-1] + enemy[0][0] > W) - 1 + (enemy[1][N-2] + enemy[1][N-1] > W)
});
break;
case 2:
dp[option][N-1] = min({
dp[option][N-2] + 2 + (enemy[1][N-1] + enemy[1][0] > W) - 1,
dp[option][N-3] + 3 + (enemy[1][N-1] + enemy[1][0] > W) - 1 + (enemy[0][N-2] + enemy[0][N-1] > W)
});
break;
case 3:
dp[option][N-1] = dp[option][N-2] + (enemy[0][N-1] + enemy[0][0] > W) + (enemy[1][N-1] + enemy[1][0] > W);
break;
}
}
cout << min({dp[0][N-1], dp[1][N-1], dp[2][N-1], dp[3][N-1]}) << "\n";
}
실행 결과 ‘틀렸습니다’ 가 떴다.
2번째 시도
기껏 만들어둔 코드가 실패하고 마음이 꺾인 나는 잠자리에 들었다… 그리고 그 다음날은 무려 군입대날이었다!
신교대, 야수교를 거치도록 좋은 아이디어는 별로 떠오르지 않았고, 자대 배치를 받고도 2달이나 넘게 지나고서야, 나는 새로운 점화식에 대한 아이디어를 얻어 코드를 작성할 수 있었다.
기존에 점화식에서 발생했던 문제는, 모든 가능한 소대 파견 방식을 고려할 수 없다는 것이었다. 그래서 아예 접근 방식을 바꾸기로 했다. ‘그리디’ 하게 최적의 연결방식을 찾는 대신, 최대한 모든 가능한 연결 방식을 고려할 수 있게 점화식을 세워보기로 했다.
새로운 점화식을 세운 아이디어는 다음과 같다.
-
dp배열의 인덱스의 의미:dp배열은 3차원 배열로 되어있다.첫 번째 인덱스는 원타곤을 일자로 폈다고 생각했을 때 첫 번째 칸들과 마지막 칸들을 ‘연결시켜’ 소대를 파견했는가에 대한 정보를 담는다.
두 번째 인덱스는 원타곤을 일자로 폈다고 생각했을 때 특정 번재 칸들과 그 이전 칸과의 연결 상태에 대한 정보를 담는다. 이것이 이번에 새롭게 작성한 점화식의 주요 아이디어다.
세 번째 인덱스는 원타곤을 일자로 폈다고 생각했을 때 특정 번재 칸들까지 점령하는데 필요한 최소 소대의 개수를 담는다. 이 때 같은 번째 칸들까지라고 하더라도 첫 번째 인덱스와 두 번째 인덱스의 값에 따라 필요한 소대의 수가 달라질 수 있다.
-
점화식 구조: 이전 칸들과의 연결 상태 및 파견 소대 수를 고려하여 현재 가능한 모든 파견 방식을 저장하도록 점화식을 구성하였다.
코드는 다음과 같이 새로 작성하였다.
#include <bits/extc++.h>
using namespace __gnu_pbds;
using namespace std;
using ll = long long int;
using ull = unsigned long long int;
using pll = pair<ll, ll>;
void simulate(void);
int main(void) {
ios::sync_with_stdio(false);
cin.tie(nullptr);
cout.tie(nullptr);
int T;
cin >> T;
for (int i=0; i<T; i++) {
simulate();
}
return 0;
}
void simulate(void) {
const int NONE_OCCUPIED = 0;
const int UP_OCCUPIED = 1;
const int DOWN_OCCUPIED = 2;
const int BOTH_OCCUPIED = 3;
int N, W, result = INT_MAX;
cin >> N >> W;
vector<pll> enemy;
enemy.resize(N);
for (int i=0; i<N; i++) {
cin >> enemy[i].first;
}
for (int i=0; i<N; i++) {
cin >> enemy[i].second;
}
// First index: Connectedness of Start and End
// Second index: Connectivity of current index
// Third index: Current index considering the circle as a line
const int LIER = 4;
vector<vector<vector<int>>> dp(4, vector<vector<int>>(4, vector<int>(N+1, INT_MAX)));
dp[NONE_OCCUPIED][NONE_OCCUPIED][0] = 2;
dp[NONE_OCCUPIED][UP_OCCUPIED][0] = LIER;
dp[NONE_OCCUPIED][DOWN_OCCUPIED][0] = LIER;
dp[NONE_OCCUPIED][BOTH_OCCUPIED][0] = 1 + (enemy[0].first + enemy[0].second > W);
dp[UP_OCCUPIED][NONE_OCCUPIED][0] = LIER;
dp[UP_OCCUPIED][UP_OCCUPIED][0] = 2;
dp[UP_OCCUPIED][DOWN_OCCUPIED][0] = LIER;
dp[UP_OCCUPIED][BOTH_OCCUPIED][0] = LIER;
dp[DOWN_OCCUPIED][NONE_OCCUPIED][0] = LIER;
dp[DOWN_OCCUPIED][UP_OCCUPIED][0] = LIER;
dp[DOWN_OCCUPIED][DOWN_OCCUPIED][0] = 2;
dp[DOWN_OCCUPIED][BOTH_OCCUPIED][0] = LIER;
dp[BOTH_OCCUPIED][NONE_OCCUPIED][0] = LIER;
dp[BOTH_OCCUPIED][UP_OCCUPIED][0] = LIER;
dp[BOTH_OCCUPIED][DOWN_OCCUPIED][0] = LIER;
dp[BOTH_OCCUPIED][BOTH_OCCUPIED][0] = 2;
for (int option=0; option<4; option++) {
for (int i=1; i<N; i++) {
dp[option][NONE_OCCUPIED][i] = 2 + min({
dp[option][NONE_OCCUPIED][i-1],
dp[option][UP_OCCUPIED][i-1],
dp[option][DOWN_OCCUPIED][i-1],
dp[option][BOTH_OCCUPIED][i-1]
});
dp[option][UP_OCCUPIED][i] = 1 + min({
dp[option][NONE_OCCUPIED][i-1] + (enemy[i-1].first + enemy[i].first > W),
dp[option][DOWN_OCCUPIED][i-1] + (enemy[i-1].first + enemy[i].first > W)
});
dp[option][DOWN_OCCUPIED][i] = 1 + min({
dp[option][NONE_OCCUPIED][i-1] + (enemy[i-1].second + enemy[i].second > W),
dp[option][UP_OCCUPIED][i-1] + (enemy[i-1].second + enemy[i].second > W)
});
dp[option][BOTH_OCCUPIED][i] = min(1 + min({
dp[option][NONE_OCCUPIED][i-1] + (enemy[i].first + enemy[i].second > W),
dp[option][UP_OCCUPIED][i-1] + (enemy[i].first + enemy[i].second > W),
dp[option][DOWN_OCCUPIED][i-1] + (enemy[i].first + enemy[i].second > W),
dp[option][BOTH_OCCUPIED][i-1] + (enemy[i].first + enemy[i].second > W)
}), dp[option][NONE_OCCUPIED][i-1] + (enemy[i-1].first + enemy[i].first > W) + (enemy[i-1].second + enemy[i].second > W));
}
}
vector<int> candidates = {
dp[NONE_OCCUPIED][NONE_OCCUPIED][N-1],
dp[NONE_OCCUPIED][UP_OCCUPIED][N-1],
dp[NONE_OCCUPIED][DOWN_OCCUPIED][N-1],
dp[NONE_OCCUPIED][BOTH_OCCUPIED][N-1],
dp[UP_OCCUPIED][NONE_OCCUPIED][N-1] - (enemy[0].first + enemy[N-1].first <= W),
dp[UP_OCCUPIED][UP_OCCUPIED][N-1],
dp[UP_OCCUPIED][DOWN_OCCUPIED][N-1] - (enemy[0].first + enemy[N-1].first <= W),
dp[UP_OCCUPIED][BOTH_OCCUPIED][N-1],
dp[DOWN_OCCUPIED][NONE_OCCUPIED][N-1] - (enemy[0].second + enemy[N-1].second <= W),
dp[DOWN_OCCUPIED][UP_OCCUPIED][N-1] - (enemy[0].second + enemy[N-1].second <= W),
dp[DOWN_OCCUPIED][DOWN_OCCUPIED][N-1],
dp[DOWN_OCCUPIED][BOTH_OCCUPIED][N-1],
dp[BOTH_OCCUPIED][NONE_OCCUPIED][N-1] - (enemy[0].first + enemy[N-1].first <= W) - (enemy[0].second + enemy[N-1].second <= W),
dp[BOTH_OCCUPIED][UP_OCCUPIED][N-1],
dp[BOTH_OCCUPIED][DOWN_OCCUPIED][N-1],
dp[BOTH_OCCUPIED][BOTH_OCCUPIED][N-1],
};
result = *min_element(candidates.begin(), candidates.end());
cout << result << '\n';
}
그러자 모든 테스트 케이스를 통과하고 ‘맞았습니다’가 나오는 것을 확인할 수 있었다.
마무리
너무 긴 싸움이었다. 입대를 하고 초반에는 금방 아이디어를 떠올릴 것이라고 생각했는데, 오히려 더더욱 미궁에 빠졌고, 자대 배치를 받을 때쯤에는 군생활 안에 풀 수 있는 문제인지 의구심이 들기 시작했다.
하지만 시간이 약이라고 결국에는 문제에 대한 좋은 아이디어가 떠올랐고, 테스트 케이스를 뜯어보며 연구한 끝에 제대로 된 코드를 만들어낼 수 있었다. CLASS 6 금장을 위한 힘찬 여정 중 난데없이 찾아온 습격자를 제대로 퇴치하는 데 성공한 것이다!
어쨌든 이 문제를 풀면서 DP가 얼마나 다양하고 창의적으로 나를 괴롭힐 수 있는지 활용될 수 있는지 제대로 배울 수 있었다. CLASS 6 에서도 주구장창 DP 문제를 풀어야 할 것 같은 예감이 든다…
오늘의 PS는 여기까지!
1: https://www.acmicpc.net/problem/1006
